矩阵的四个基础子空间

这是十周年重修工科数学系列课程之… 线性代数基础。重修这件事，有效缓解了焦虑和失眠，让自己觉得，生活除了吃饭睡觉和~~想象空间愈发匮乏的~~工作，还是有一些其他内容的。

向量空间和其（线性）子空间的定义

线性空间需要满足加法封闭和数乘封闭：

加法封闭（可加性）: 空间内任意两向量相加（减），结果必须还在空间中： $a \in \mathbb{R}^n, b \in \mathbb{R}^n \Rightarrow (a+b) \in \mathbb{R}^n$
数乘封闭（齐次性）: 空间内任意向量乘以标量，结果必须还在空间中： $a \in \mathbb{R}^n, \lambda \in F \Rightarrow {\lambda}a \in \mathbb{R}^n$

注意“数乘封闭”隐含了：线性空间必须包括零向量（当 $\lambda = 0$ 时）；因为线性变换不研究坐标系原点的移动（假设所有向量都从同一原点出发）。

确立一个线性空间子空间需要知道：

空间的维数（假设为 $n$ ）
空间中一组 $n$ 个线性无关的向量，称为基（basis）

线性空间的两个封闭要求刚好对应了向量的两种线性组合方式，所以可以理解子空间是由基向量所有的线性组合张成（span）的向量空间。

基的正交标准化

空间的基不要求正交和模长为 1，但是如果它满足这两点，会更方便计算。对应的术语是正交化（orthogonal）和标准化（normal），两点都具备时可以用合成词正交标准化（orthonormal）称呼。

有意思的是，我阅读了一些书籍和维基百科，得知根据以上向量空间的定义，“长度”和“夹角”并不是一个向量空间的内禀特性。我们需要额外引入“内积”的定义，即让两个向量点乘之后得到一个标量，才借此产生了模长和夹角，进而可以定义什么是标准化（模长为 1）和正交化（夹角垂直）。引入了内积的线性空间称为内积空间。

当然高维空间不能像二维或者三维空间那样直观地想象长度、夹角乃至夹角垂直，但是可以根据向量和自己的内积来定义模长的平方，根据两向量内积为 0 来定义垂直。

代数方法研究向量空间往往不强依赖坐标系统，但是如果引入坐标轴，套用二维或者三维空间的几何意义，那么最常见的一组标准正交基就是坐标轴上的单位向量。以其为列向量合成矩阵，即得到仅对角线为 1 其他位置都是 0 的方阵——单位矩阵（identity matrix）。

矩阵的四个基本子空间的定义

先要非正式地定义一下矩阵的秩：秩（rank）即矩阵最大线性无关组中包含的向量数 —— 刨除所有因为和其他向量线性相关，而在作为基向量的时候对张成空间的维数“毫无贡献”的向量之后，剩下的有效向量数目。

无论是否是方阵，都可以根据行向量或者列向量是否线性无关，来得到行秩和列秩。行秩一定等于列秩，不在这里证明这一点。但知道这一点时，仅取行秩或列秩就可以知道矩阵的秩。

假设 A 是 $m \times n$ 的矩阵，其秩为 $r$ ：

列空间（column space）

A 中所有列向量张成的子空间，维度是 r，记作：

$C(A) = Span\{v = \sum_{i=1}^m{\lambda_i}{c_i}|v \in \mathbb{R^{r}}, \lambda \in F, c_i \in \text{column vectors of A} \}$

行空间（row space）

A 中所有行向量张成的子空间，维度是 r，记作：

$C(A^T) = Span\{v = \sum_{i=1}^n{\lambda_i}{r_i}|v \in \mathbb{R^{r}}, \lambda \in F, r_i \in \text{ row vectors of A} \}$

零空间（nullspace）

以 A 为系数矩阵的齐次线性方程组的所有非平凡解集张成的子空间，说人话就是“能令 Av = 0 的所有非零 v”：

$N(A) = Span\{v|v \in \mathbb{R}^{m - r}, Av = 0\}$

左零空间（left nullspace）

类似列空间和行空间的关系，左零空间是 A 的转置的零空间；“左零”的说法来自其定义中矩阵是“左乘”到向量上的，而不是习惯上的右乘：

$N(A^T) = Span\{v|v \in \mathbb{R}^{m - r}, v^TA = 0\}$

非奇异（可逆）矩阵的子空间

矩阵非奇异（可逆）的充分必要条件是矩阵的行、列数都等于其秩，即满秩矩阵。无论是行向量之间，还是列向量之间，都线性无关——矩阵中的每一行都为行空间贡献了维度，每一列都为列空间贡献了维度。

正因如此，非奇异矩阵的零空间和左零空间就成了零维的——其中只包含零向量（参考定义中关于子空间维数）。非正式地说法可以是“非奇异矩阵没有零空间和左零空间”。

实际上两个行列空间和两个零空间构成某种补集关系，见下节。

行列空间和零空间的正交补关系

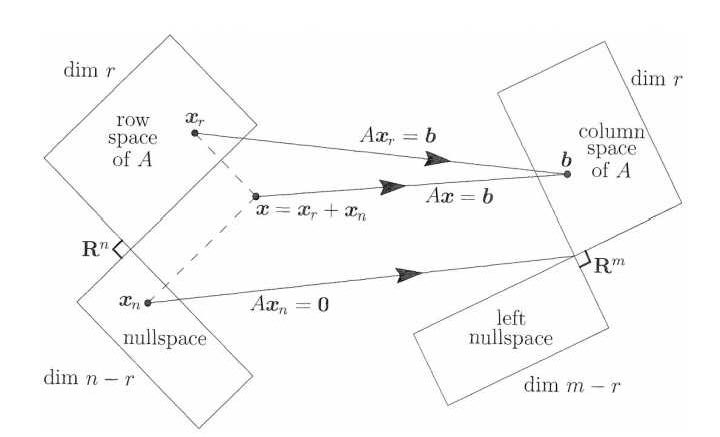
这张出处不详的图，很好地描述了四个基本子空间的关系。维系这个关系的关键动作，在于矩阵被用于线性变换（线性映射）。

Ax = b

上述线性方程组的矩阵写法，可以诠释为矩阵 $A$ 对（作为未知数集的） $x$ 向量进行了线性变换，产生了向量 $b$ 。

这个变换的过程中，向量 $x$ 来自 $A$ 的行空间或零空间（左侧的两个空间），变化后到达列空间。因为按照矩阵乘法的定义， $b$ 一定是 $A$ 中各列按照 $x$ 的线性组合（或者说以 $A$ 中各列为基， $x$ 的坐标表示）。

对于非奇异矩阵，因为它是满秩的，行空间足以张成整个 $\mathbb{R}^n$ 空间，列空间足以张成整个 $\mathbb{R}^m$ 空间（假设 $A$ 是 $m \times n$ 的矩阵），那么行空间中所有向量一定可以一一映射到列空间中，行空间中零向量也只映射到列空间的零向量上。

对于奇异矩阵，因为行空间中存在浑水摸鱼的向量，其只能张成 $r$ 维空间（ $r < n$ ），剩下的 $n - r$ 维构成了零空间，零空间中的向量可能不是零，但在 $A$ 的线性变换作用下却映射到列空间的零向量上，即方程说的 $Ax = 0$ 的非平凡（ $x$ 不为 0 的）解。

也就是说，零空间中的任何向量，和 $A$ 的任何一个行向量的内积都是 0，按照内积空间的定义，它们正交。整个零空间和整个行空间构成正交补的关系。引用 Dante 老师的话：

行空间的正交可以理解：它的 nullspace 就是跟行空间垂直的向量组成的

在上面这个变化过程中，左零空间没有参与。其实可以将 A 转置来得出类似于“行空间正交于零空间”的结论，列空间也正交于左零空间。

x^TA = b^T

这个变换其实是将右乘的线性变换两边转置，以交换 $A$ 的行和列。此时行向量 $x$ 存在于列空间中或左零空间中。若 $x$ 存在于列空间，则在矩阵左乘的变换下映射到行空间中的 $b$ ；若 $x$ 存在于左零空间中，则在矩阵左乘的变换下映射到零向量。

其他的称呼

矩阵可以表示线性变换（一般习惯还是用右乘，即矩阵在左向量在右），在语境为线性变换的时候，列空间和零空间有别的称呼：

列空间称为线性变换的“像”（image）
行空间称为线性变换的“原像”（preimage）
零空间称为线性变换的“核”（kernel）

非常的形象了，零空间变换后是要坍缩成一个点（零向量）的，不就是“核”么。

用到左零空间的地方

看起来左零空间在（正向的）线性变换中根本不出现，而且只是列空间的正交补，比较没有意思。

不过往后学习一点，还是会用到的。默认在定义矩阵的逆的时候，只对可逆的方阵（非奇异）才有意义，因为可逆矩阵的零空间真的是个零（只有零向量），那么行空间中每个向量都可以一一映射到列空间中，自然映射也就可逆——找出逆矩阵，将原矩阵列空间中的向量再映射回行空间。

对于奇异矩阵，因为零空间的存在，零空间中的非零向量会被矩阵映射到零向量上。那么无论如何，我们都没法再找出一个矩阵，能把零向量映射回原零空间中的非零向量了——变成零后信息已经丢失了。这也是“不可逆”的原因。

但是对于不可逆的矩阵（可以是奇异方阵，甚至可以是长方矩阵），可以定义其“伪逆”（pseudo-inverse），即在正向变换的时候，仍然是行空间映射到列空间，零空间映射到零向量；逆向变换的时候，将列空间映射回行空间，左零空间则映射到零向量。

Ax = b\ or\ 0 \text{ then } A^+b = x\ or\ 0

嗯… 就是接受有的分量（在左零空间）中会丢失（退化）这件事，因为反正它们也是从零空间来的。所以伪逆的概念里蕴含了某种投影的思想…

这个在最小二乘法里比较有用，因为反复收集数据很可能因为数据重复导致矩阵奇异。这个时候我们希望“浑水摸鱼的向量就不要出声”，求伪逆当作逆用就好。

求伪逆的方法，其中一种是对矩阵 $A$ 做奇异值分解（SVD），将其变成两个正交矩阵和一个对角矩阵的乘积。正交矩阵一定可逆，其伪逆就是其逆；对角矩阵如果对角线不含零元素（对角矩阵也可逆），求逆时取对角线元素的倒数即可；不可逆矩阵的 SVD 中，对角矩阵一定含有零元素，那么求伪逆时只对非零元素取倒数，零元素仍然取零（对应左零空间仍然映射到零向量），得出对角矩阵伪逆。再将三个逆和伪逆重新合成，得到 $A$ 的伪逆。

线性方程组的通解和特解

线性方程组的通解为什么等于特解加上零空间的向量，就可以解释了。因为零空间中的向量在线性变换中中只产生零向量，根据线性变换基本法：

T(a + b) = T(a) + T(b)

T(a + b) = T(a)\ \ if\ \ T(b) = 0

来自零空间的 $b$ 对线性变换没有贡献，带上它才能在“值域”不变的情况，让“定义域”完整。

无知的 tonyseek

Yet Another Seeker